1. SUMMARY/OBJECTIVE

In 1632 Galileo proposed a simple gravity experiment that has not yet been carried out. My primary objective is to generate interest in fulfilling Galileo’s proposal, so that his experiment is duly performed. In three different passages in his Dialogue Concerning the Two Chief World Systems [University of California Press, 1967; pp. 22, 227, 236] Galileo wondered what would happen “if the terrestrial globe were pierced by a hole which passed through its center, [and] a cannon ball [were] dropped through [it].”

Drilling a hole through Earth is obviously impractical or impossible. But the experiment’s significance would be just as well demonstrated using smaller bodies in an orbiting satellite or an Earth-based laboratory.

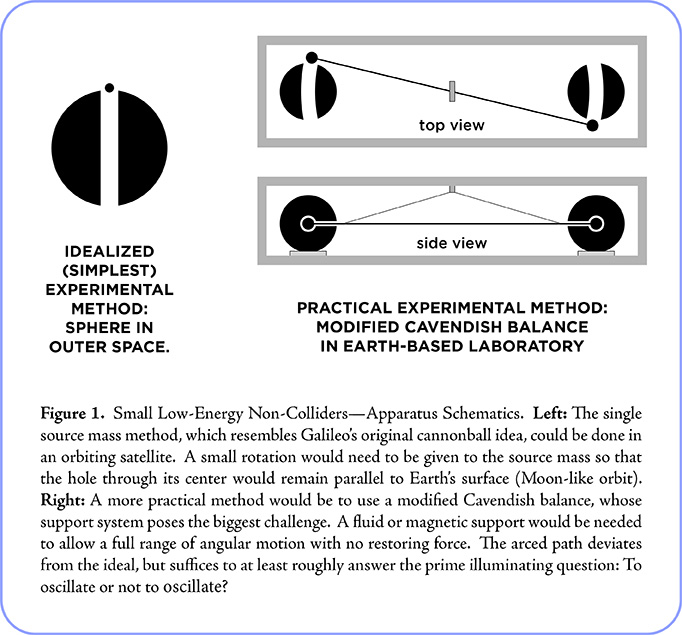
Collisions of stupendous energy-density—comparable to that of the hypothetical Big Bang birth of the Universe—are routinely produced by the biggest, most expensive machine on Earth: the Large Hadron Collider. At the opposite extreme, Galileo’s experiment involves the small gravitational energies of ordinary bodies of matter, configured so that a small one falls radially with respect to the center of a larger one without ever colliding. The idea is thus to allow the uninterrupted unfolding of the simplest conceivable gravitational interaction between two bodies of matter, and to observe the whole process, using an apparatus aptly called a Small Low-Energy Non-Collider. Two basic designs are schematically depicted in Figure 1.

Figure 2  provides further comparison between high-energy collision experiments and low -energy non-collision experiments. Figure 3  graphs the contrast between our knowledge and ignorance of gravity-induced radial motion outside and inside material bodies. By neglecting to build and operate a Small Low-Energy Non-Collider, physicists say, in effect: “We already know how to complete the graph for this experiment without actually doing the experiment.” In other words, they cheat on the empirical ideals of science.

This attitude is reflected in dozens, hundreds, or thousands of papers, textbooks and physics classrooms, where the result of Galileo’s experiment is routinely presumed to be “well known.” Since no empirical evidence is ever provided to support this presumption, Galileo’s experiment is clearly overdue to be carried out. The ideals of science dictate that claims of physical knowldege are to be supported by repeatable experiments. (Nullius in verba.) The predicted result of Galileo’s experiment has not yet been supported even once.

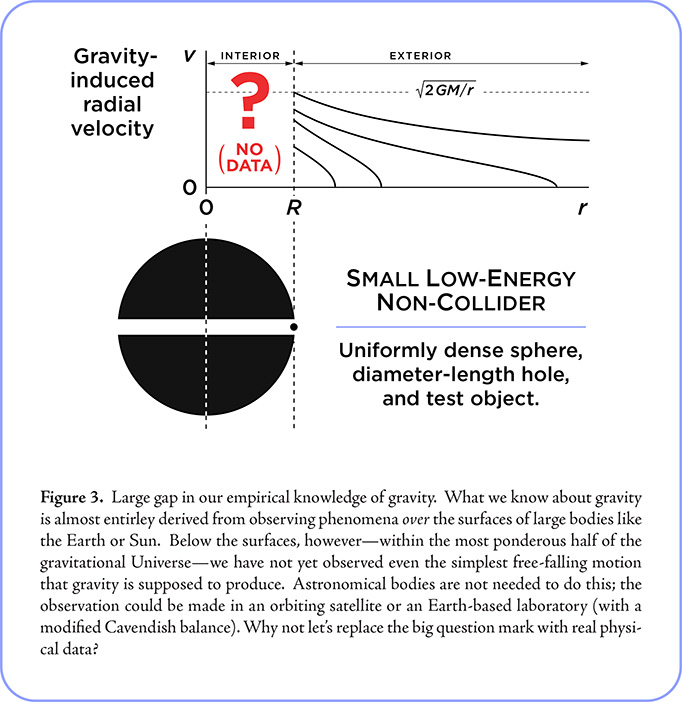
Modern physics has invested heavily in exotic, yet never observed forms of matter and in exotic, yet never really observed black holes. Curiously, this illustrious pinnacle of the sciences has so far neglected to make the much simpler, much less costly investment to actually observe an ordinary body of matter as it falls undisturbed into an ordinary hole through the center of an ordinary larger body of matter. Especially given how enigmatic gravity is sometimes admitted to be, this is surely one of the most ironic facts about the state of modern gravitational physics. There is no good reason to continue neglecting to test the interior solution.

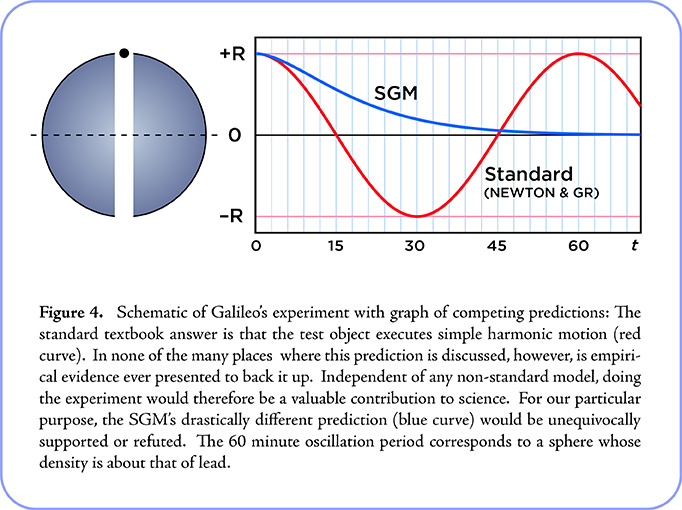
The line of inquiry pursued below suggests that, when the test of the interior solution (Galileo’s experiment) is finally carried out, the standard prediction will not be supported. The standard prediction is that the smaller body will have a maximum speed as it passes the center and will oscillate back and forth between the hole’s extremities forever. The prediction based on the new hypothesis (presented below) differs drastically in that the smaller body does not pass the center. (See Figure 4.)  This hypothesis is called the Space Generation Model (SGM).

To be viable, any new gravity model must agree with the many observations that support the reigning theory of gravity, Einstein’s General Theory of Relativity (GR). This is done for the SGM in a few of the papers listed at left, especially Maximum Force, and Speed of Light and Rates of Clocks.

2. COSMOLOGICAL IMPLICATIONS

The latter document features extended sections on how the SGM relates to atomic physics and cosmology. The most noteworthy result of this work is how it leads to a simple expression that connects Newton’s constant $G,$ to the other constants of physics. The first of the three quoted statements (at left) affirming the fact of $G$’s aloofness from the rest of physics poignantly begins:

“$G$ stands mysteriously alone.” — G. T. Gillies [1]

(See also [2] and [3].) In hopes of solving the mystery and bringing $G$ into the fold, I. J. R. Aitchison has recommended exploring ways that it might be related to the other constants:

“Could the dimensions of Newton’s gravitational constant be explained... by a theory of gravity characterized by a fundamental mass (or length) and a dimensionless strength? Could we then unify all the forces? Something new is needed.” [‘The Vacuum and Unification,’ in The Philosophy of Vacuum. (Clarendon Press, 1991) pp. 185–186.]

In the SGM-based expressions to follow, $c\,$ is the speed of light, $\mathrm{a}_{{\small \mathrm{o}}}\,$ is the Bohr radius, and $m_{{\small \mathrm{e}}}\,$ is the electron mass. These constants combine to form the dimensioned part of $G$ (acceleration of volume per mass). The dimensionless strength is a ratio of densities: The mass-equivalent of the cosmic background radiation, $\rho_{\mu }\,$ and the nuclear saturation density, $\rho_{\scriptsize \mathrm{N}}\,.$ Altogether, we find

\begin{equation} \hspace{127pt} G = 8\left(\frac{\rho_{\mu }}{\rho_{\scriptsize \mathrm{N}}}\cdot\frac{c^2\mathrm{a}_{{\small \mathrm{o}}}}{m_{{\small \mathrm{e}}}}\right) \,. \hspace{127pt} \end{equation}

Notice that all three desiderata of Aitchison are fulfilled.

Showing more comprehensively how $G$ relates to other constants in quantum theory, the above expression may be equivalently written:

\begin{equation} \hspace{39pt} G = 8\left(\frac{\rho_{\mu }}{\rho_{\scriptsize \mathrm{N}}}\cdot\frac{c^2\mathrm{a}_{{\small \mathrm{o}}}}{m_{{\small \mathrm{e}}}}\right) = \frac{4}{\pi \alpha}\left(\frac{\rho_{\mu }}{\rho_{{\scriptsize \mathrm{N}}}}\cdot\frac{h c}{m^2_{{\small \mathrm{e}}}}\right) = \displaystyle{\frac{1}{2}} \alpha^3 \left(\frac{\mathrm{a}_{{\small \mathrm{o}}}}{R_{\small \mathrm{C}}}\cdot\frac{c^2 \mathrm{a}_{{\small \mathrm{o}}}}{m_{{\small \mathrm{p}}}}\right)\,, \hspace{39pt} \end{equation}

where $h$ is Planck’s constant; $\alpha$ is the fine structure constant, $m_{{\small \mathrm{p}}} $ is the proton mass, and $R_{\small \mathrm{C}}$ is the SGM’s cosmic radius. Nuclear saturation density ($\rho_{\scriptsize \mathrm{N}}\approx 2.84 \times 10^{17}\,$ kg/m$^3$) is the least well known of these quantities. But many estimates of its value (uncertainty $\approx\,\,$6%) are such as to make these expressions for $G$ perfectly consistent with measurements. If this is not just a coincidence, then they represent a big step toward the unification alluded to by Aitchison.

Illustrating the possible importance of these connections, especially with regard to the role of the fine structure constant, is a figure in the Speed of Light and Rates of Clocks essay. Figure 27 from the essay is called a Cosmic Everything Chart because, on logarithmic scales, it represents all massive bodies in the Universe and their densities, including the Universe itself. The Chart makes graphically evident a variety of universal patterns whose significance is independent of the SGM, patterns that are nevertheless more intuitively comprehensible from the SGM point of view. We will return to some of these cosmological consequences before concluding this article.

The most important fact about our new model is its clear-cut testability. The SGM is not just a new interpretation of existing theory, nor a model whose testability lies beyond or at the extremes of our technological reach. Whether the SGM curve in the above graph (Figure 4) corresponds to physical reality or not, can be determined by conducting the simple experiment that Galileo proposed 384 years ago. If the local behavior of gravity—as revealed inside matter, where we have not yet looked—corresponds to the SGM prediction, this will lend strong support for the global, cosmological expressions presented above.

3. BASIS of the SPACE GENERATION MODEL:
ACCELEROMETERS, CLOCKS,
and EINSTEIN’S ROTATION ANALOGY

3.1. Introduction; Potential Scope. Having jumped from Galileo’s belated gravity experiment all the way to the cosmological implications of the SGM’s non-standard prediction, let us now deliberate on a few of the key steps in between. Why else might we expect the SGM to ring true? Constructive answers will be given in due course, but we will begin by presenting some evidence that the current state of fundamental theoretical physics leaves much to be desired. The evident and sometimes explicitly stated uncertainty, incompleteness, and even confusion characterizing this state gives the impression that transcending it may require some radical thinking and surprising discoveries.

The difference in predictions (as revealed in the above graph) may seem so extreme as to warrant immediate dismissal: Surely the prevailing conceptions of gravity cannot be that far wrong! Reasonable as this guess may be, it is only a guess. The definitive decision on the matter—to qualify as a scientific decision—requires the empirical experiment to be actually carried out. If the result of Galileo’s experiment were to agree with the SGM’s prediction, it would indicate problems with a lot more than prevailing gravity theories. Other large parts of physics and cosmology would also be in for unprecedented upheaval.

The literature of physics happily includes some self-critical comments exhibiting a range of dissatisfaction with prevailing theories. These comments sometimes portend upheaval—but the anticipated changes are nowhere near as radical as what would be engendered by the SGM, if Galileo’s experiment should support it.

The deepest problems in physics are conceptual, not mathematical. Given the plethora of mathematically inclined physicists inhabitaing academia, it is reasonable to surmise that if the problems were mathematical, they would have been solved long ago. Physicists have been trained to think of physics problems as math problems.  A common cliché is that of the stern professor ordering his conceptually groping students to “shut up and calculate!” This is arguably a big part of the problem. Stating it in terms of a dichotomy between “craftspeople” (math-inclined physicists) and “seers” (rebelious, creative, idea people), physicist Lee Smolin inquires:

“Are we asking the right questions?... We are missing something big... Every physicist I know will agree that probably at least one big idea is missing.

“Even if everyone can see that a revolution is necessary, the most powerful parts of our community have forgotten how to make one... It is a fantasy to imagine that foundational problems can be solved by technical problem solving within existing theories.

“We are horribly stuck, and we need real seers, and badly... [Seers] can be recognized by their rejection of assumptions that most of the rest of us believe in.”

[The Trouble With Physics (Houghton Mifflin, 2006) pp. 308, 311, 312, 314.]

After decades of study by thousands of physicists, the biggest problems remain virtually unscathed. Mathematical methods of attack thus appear as prime suspects for the failure. As implied by Smolin, it appears  that all physicists have been trained to believe in some fundamental concept or combination of concepts that is ultimately wrong.

This training is evidently so deeply entrenched, is such a matter of unquestioned Faith, that the idea of conducting a simple experiment (i.e., Galileo’s) to empirically test this Faith in the physical domain inside matter where we have not yet looked, remains an unsuspected blind spot. Refusal to carry out the experiment represents a kind of self-induced deprivation of data: Another test of Faith, not in understanding of the physical world, but in sociological allegiance to group-think “knowledge,” in collectively pretending to know something that is not really known. This is surely one of the gravest errors scientists can make—no matter what the result of the experiment may ultimately be when someone finally gets around to performing it.

How this state of affairs could come about is suggested by the following observation from a different field of academia:

“Fundamental challenges to disciplines tend to come from outside. It is customary for students to be introduced to their fields of study gradually, as slowly unfolding mysteries, so that by the time they can see their subject as a whole, they have been so thoroughly imbued with conventional preconceptions and patterns of thought that they are extremely unlikely to be able to question its basic premises.”

[Martin Bernal, Black Athena: The Afroasiatic Roots of Classical Civilization, vol. 1, 1987.]

By the following comment, John A. Wheeler implicitly echoes the perception that fundamental physics is stuck in a conceptual rut:

“To my mind there must be, at the bottom of it all, not an equation, but an utterly simple idea. And to me that idea, when we finally discover it, will be so compelling, so inevitable, so beautiful, that we will say to one another, how could it have been otherwise?”

[Video interview in Creation of the Universe, Timothy Ferris, PBS, 1985.]

Among the problems that Smolin and Wheeler have alluded to—big, fundamental, outstanding problems that have resisted solution for many years—are those concerning:

1. The nature of Time, and its irreversible arrow.

2. The nature of Inertia (Mass)—which physicists think they can discover by tweaking and cranking up the juice in their high-energy collision experiments. (New Scientist writer Stuart Clark has written that “no one has yet come up with a convincing explanation of inertia.” Quoting Cambridge University physicist Ben Gripaios, the article continues: “We do not yet know how to define [inertia]...We know it must be related closely to mass, but until we can define it precisely and know how to measure it, there can be no theory for it.” — [19 January 2013, p 34.])

3. The nature of Space and its possible extra-dimensionality.

4. The problem of “Unification”—which is seen as having to do with the state of the Universe near its alleged beginning—which is assumed to involve scales of size and energy many orders of magnitude smaller or larger than those pertaining to the actually observable state of the present Universe.

5. Other problems concerning singularities, infinities, instabilities, hypothetical dark matter, dark energy (also known as the “Cosmological Constant problem”) and so on.

If the SGM is basically correct, then all of these problems will certainly be in need of reassessment. Some of them will be convincingly solved: For example, the problems of Time, Space Dimensionality, Inertia, and Dark Energy.

To say that the stuck state of fundamental physics is in need of a fresh concept to get itself unstuck is not to say that the solution will not correspond to its own mathematical expressions. We have already presented one of the key mathematical consequences of the SGM, and more will follow in due course. But our main focus will be the concepts themselves, the communication of which is often facilitatied by graphic illustrations.

With that preamble, to establish the reasonableness of expecting Galileo’s experiment to yield a non-standard result, let us now embark on the following perspective-shifting exercise in imagination.

3.2 Accelerometers, Clocks, and the Speed of Light. The way we perceive the physical world is inevitably colored by our immediate environment and by conceptions of it that we’ve inherited through many generations of human existence. Our home is a $5.97 \times 10^{24}$ kg ball of matter. Primitively conceived as the immense and immovable center of the Universe, an imagined characteristic of our planet that has persisted from ancient to modern times is its staticness. We know, of course, that Earth spins, orbits the Sun, and that its constituents undergo a wide range of geological transformations; we know that at the atomic and molecular level, Earth’s matter never stops moving. And yet, with regard to gravity, the assumption of staticness prevails. In Newtonian gravity the staticness of the dominant body of our consideration (e.g., the Sun or Earth) is usually implied. Whereas in GR the solution of Einstein’s equations pertaining to such cases is often explicitly stated as being a static geometrical object: i.e., the Schwarzschild exterior solution. A patently static chunk of stuff somehow warps spacetime and somehow causes other chunks of stuff to move. This enigmatic somehow embodies the stubbornly persistent, typically ignored, yet still unsolved mystery of gravity.[4-10]

Contrary to the prevailing tradition, we assume that the somehow, i.e., the mechanism by which matter warps spacetime, ought not to be smuggly ignored, but rather deserves serious attention. We begin by questioning the assumption of staticness. To see the preconception of staticness as being not at all obvious, but as logically very questionable, in what follows we will contemplate and frequently adopt the perspective of a hypothetical alien civilization: intelligent beings who are not from Earth nor any other planet. Instead, they have evolved on a large (but comparatively light) rotating space station far from any astronomical bodies of matter. (See Figure 5.) Their wheel-like abode, called Roton, is the size of a large Earthian city, but its mass/radius ratio is so small that any effects of gravity (as we seemingly “know” them) have remained unnoticed. [Note that an abbreviated version of this “Rotonian” scenario is found in Rethinking Einstein’s Rotation Analogy.]

Though having no conception of gravity, the society of Roton is otherwise advanced. Their scientific instruments are extremely reliable and capable of measuring small changes in distance, velocity, acceleration, and clock frequency. Also Rotonian mathematicians are well versed in non-Euclidean and higher-dimensional geometries.

Presently, the Rotonians are planning an excursion to investigate the mystery of the distant myriad points of light that have filled their dreams for as long as they can remember. Before chronicling their adventure, let’s take stock of the Rotonians’ understanding of motion. Aside from telescopes, gyroscopes and various complex inertial guidance systems, two of their most basic motion-sensing devices are accelerometers and clocks. Accelerometers stationed at various distances between the hub and rim of Roton inform them of the force experienced by bodies at these positions. When exploring their exterior neighborhood, accelerometers serve just as reliably to indicate the propulsive force of their rockets. A key fact ingrained in all Rotonians is that accelerometers are utterly reliable gauges of acceleration. If an accelerometer gives a non-zero reading it means the device is being forced to move in the indicated direction with the indicated magnitude. Especially noteworthy is that, to a Rotonian, if an accelerometer reading is zero, the instrument is certainly not accelerating. (See [11] at left.)

Rotonians understand clocks to be motion sensing devices unto themselves because of their change in frequency due to velocity. Clocks are thus key components of more complex and sophisticated communications and positioning systems. Roton is equipped with an array of synchronized clocks and electromagnetic wave relays. The most sensible method of clock synchronization, which they have adopted, is by way of a signal from the axis. Early in the development of this system Rotonians discovered a crucial asymmetry. With respect to their physical world, the speed of light in one direction of motion is faster than the constant, $c\,,$ and in the opposite direction it is slower than $c\,.$ Given that $r$ is the distance from the axis and $\omega$ is the angular velocity, the unchanging speed of rotation (stationary tangential velocity) is the product $S_{\scriptsize{ROT}} = \,r\omega\,.$ The measured tangential speed of light (to first order) is then $\, \bar{c} = c \pm r\omega\,.\,$ Since some of the Rotonians’ communication and positioning needs are most demanding, if this light-speed asymmetry were not taken into account, serious accidents could occur. For a given rotation speed, at a given radius, the rod-measurable distance around the circumference is a constant, regardless of the direction such measuring takes place. And yet the transmission of light around the circumference is decidedly direction-dependent: it is slower than $c$ (even at first order) in the direction of rotation, and faster than $c$ in the opposite direction.

Earthian readers who may have the impression that the speed of light is always the same in any direction should bear in mind that the synchronization method of our Global Positioning System is essentially the same as the Rotonian one, for the same reason. It takes account of the asymmetry in light speed due to Earth’s rotation. Havoc would prevail upon Earth if we had fancied to “synchronize” clocks by the Einsteinian prescription, one-by-one around the circumference. More sophisticated Earthian readers may think, yes this is true, but the speed of light is at least “locally” equal to $c$ for all Einstein-synchronized observers. As it turns out, Rotonians never got the memo giving the order to obey this chaos-inducing stipulation; nor have they ever suffered for it. So we’ll continue with their story.

3.3. Maiden Voyage. For many centuries Rotonians have had their array of clocks in place. It includes one at the axis, many along the rim, and many in between. Careful observation of these clocks has provided the Rotonians with ample evidence of the effect of velocity on the rates at which clocks tick, i.e., their frequencies. Faster tangential speeds correspond to slower clock rates. Since this speed varies as the radial distance, the fastest clock in the system is the one at the axis, where the tangential speed is zero. Clocks have proven themselves as motion-sensing devices not only when rigidly stationed on the structure of Roton, but also in the (somewhat trickier) case of linear velocity, as when they venture beyond Roton’s confines. For the sake of brevity we need to omit other aspects of the Rotonian understanding of motion, light, space and time. Suffice it to say that accelerometers and clocks will play the most significant role as motion-sensing devices in what follows.

The day finally comes for our intrepid explorers (and “gravity virgins,” as it were) to embark on their journey to parts unknown. Fast forward many years: The Rotonians awaken from their pre-arranged stasis to find themselves nearing what they eventually learn is a “planet” called Earth. What a bewildering experience! This colossal ball of matter appears to be accelerating toward them with ever increasing magnitude. They know they are not accelerating toward the planet, because their rockets are off; their accelerometers read zero. In the nick of time they turn around and blast their rockets so as to accelerate upwardly and make a soft landing.

Imagine the Rotonians’ astonishment when they learn that the acceleration of the planet toward them would have been the same from any angle of approach. Accelerometers all the way around the globe say that its surface is “coming up.” From their Earthian hosts, the Rotonians learn that this effect is called gravity. What they do not understand is why the natives think of the planet as being static. Most Earthians say that a “falling” accelerometer, whose reading is zero, actually accelerates downward. This strikes the Rotonians as utter nonsense.

Nor does the impression of nonsense dissipate when told by a certain faction of Earthians that positive accelerometer readings do indeed mean the ground is accelerating upward, because even this faction (General Relativists) still regards the Earth as a whole as static.[11] Earthians, the Rotonians surmise, are schizoid.

3.4. Resolution by Experiment. Being conscientious and compassionate scientists, Rotonians are eager to gather evidence to settle the matter. The stakes are clearly high, as it is in the blood of any Rotonian to regard non-zero accelerometer readings as indicating only one or a combination of two things:

     1. Rotation and/or

     2. A source of propulsion.

Now they need to admit the possibility—depending on the results of their investigation—that they must add:

     3. A state of rest (e.g., rigid contact) with respect to a nearby, typically large, massive body.

Since rotational acceleration always produces negative (toward the axis) accelerometer readings and accelerometer readings on Earth’s surface are everywhere positive (outward), the dominant motional effect of the planet is obviously not rotation.

Rotonians are instinctively loath to entertain the idea that positive accelerometer readings should be associated with a state of “rest.” But they admit they need more evidence to be sure their instincts ring true. As witnesses to this drama, are we to accept Earthians’ ancient contradiction-laden belief in static chunks of stuff, or Rotonians’ belief in the consistent truthfulness of accelerometer readings? One of these views must clearly be in error.

Rotonians suspect that the crucial evidence lies inside the planet, or in principle, inside any body of matter—under the hood, so to speak. In accordance with the possibilities mentioned above, they instinctively suspect that matter manifests itself as a source of perpetual outward propulsion. How else could a material body maintain constant positive (non-rotational) accelerometer readings all around its surface? The possibility that matter behaves this way did not occur to Rotonians earlier because they had not before encountered such an enormous concentration of it. The possibility did not occur to Earthians earlier because their conception of the world had been (and continues to be) more heavily influenced by their primitive visual impression of staticness. Like water to a fish, the ubiquitous tactile evidence of accelerated motion either goes unnoticed or gets swept under the carpet of mathematical formalism.

In terms of their unforgettable landing experience, Rotonians want to determine what would have happened if, instead of landing on the surface, their approach had taken them into an evacuated hole through the planet, to fall (rockets off) as far as they would, toward the center. Obviously this can’t be done with the planet itself, but it could be done in a laboratory with much smaller bodies. Having learned from Earthian archives that Galileo proposed the experiment 384 years ago, Rotonians give Galileo credit by naming the experiment after him. Extreme contrast with the kinds of experiments that Earthians have made their favorites inspires Rotonians to call the apparatus needed to conduct Galileo’s experiment a Small Low-Energy Non-Collider.

From the Earthian theory of gravity Rotonians have learned of the oscillation prediction for Galileo’s experiment. If this prediction were correct it would substantiate (3.) above. Their own prediction, which is based on their trust in accelerometer readings, is that the test object will not fall past the center (as in Figure 4). Rotonians think it is obvious that nothing ever pulls the object downward. Being surprised that Earthians had not thought of testing their oscillation prediction before, the Rotonians are delighted to bring the possibility to their attention. Happily, the mere presence of the friendly alien Rotonians has induced a new sense of mental flexibility amongst Earthians. With abundant enthusiasm Earthian scientists join the Rotonians in their experimental pursuit.

4. CONNECTION to SPECIAL and GENERAL RELATIVITY:
STATIONARY MOTION and
the DIMENSIONALITY of SPACE

4.1. Gravitational Research. As plans to do the experiment get underway, Rotonian theorists eagerly absorb all they can about Earthian ideas of gravity and motion. They especially seek out what is common to both worlds. But they do not shy away from certain prominent conflicts. Accepting at a fundamental level that motion-sensing devices always tell the truth, Rotonians are driven by instinct to question some deeply entrenched elements in the Earthians’ Relativity-imbued conception of the physical world.[12] We will address some of these conflicts below.

Let us begin, however, with a profound element of agreement. Of particular importance is the Rotonians’ discovery in Earthian archives concerning the Special Theory of Relativity of a particular mathematical expression for the fact that the speed of light is a physical limit. From their own experiments with light, clocks, and the effect of velocity thereon, Rotonians had long ago derived an identical equation. Its meaning is as follows. If a rocket is provided with a huge fuel supply allowing it to maintain the same acceleration for a very long time, its velocity will continually increase, but cannot reach the speed of light. The equation is

\begin{equation} \hspace{131pt} v(t)=\frac{at}{\sqrt{1+a^2t^2/c^2}}\,\,, \hspace{131pt} \end{equation}

where $a$ is the acceleration as indicated by an onboard accelerometer and $t$ is the time given by a clock in the original reference frame. Eq. 3 and its connection to two other equations, to be presented momentarily, serves to reinforce and give mathematical expression to the analogy between uniform rotation and gravitation. We’ll return to this equation below.

Unknown to the Rotonians before their trip to Earth is the significance of Newton’s constant $G.$ To make concrete sense of it they imagine Earth as having planted upon its surface an array of extremely tall towers extending vertically many diameters into space. (See Figure 6.) From the Earthian theory, they find especially significant that, if they had never fired their rockets for a soft landing—i.e., if they had only just “fallen” to Earth (and neglecting the effect of the Sun and other planets) with rockets off, then the relative speed between points along one of these towers and their rocket would have been $\approx \sqrt{2GM/r}\,,$ where $M$ is the mass of Earth and $r$ is the distance from the center. Corresponding to this speed is the acceleration $g\approx GM/r^2.$ Accelerometers placed at various locations along the tower confirm this well known inverse-square pattern of acceleration. And clocks fastened alongside the accelerometers are found to have frequencies that vary as

\begin{equation} \hspace{124pt} f(r)\approx f_{\small 0}\sqrt{{ 1- \frac{{2GM}}{{rc^{2}}} }}\,, \hspace{124pt} \end{equation}

where $ f_{\small 0}$ is the rate of a clock at infinity. Note that the argument of the coefficient in Eq. 4 contains the square of the velocity indicated above, i.e., $2GM/r\,.$ Also note that GR predicts this equation to be exact, not just approximate. Whereas the hypothesis the Rotonians are beginning to develop leads them to a different exact expression, as we will see later. For most circumstances the differences are extremely small. Eq. 4 is clearly analogous to the corresponding equation involving rotation:

\begin{equation} \hspace{126pt} f(r)= f_{\small 0}\sqrt{1- \frac{{r^{2}\omega^{2}}}{{ c^{2}}}}\,. \hspace{126pt} \end{equation}

In both cases the argument of the coefficient is a speed squared ratio. In both cases the speed of all points within the system has a well-defined dependence on radial distance, and the rates of clocks vary correspondingly. These equations and the motion-sensing instruments in Figure 6 clearly show the effects on accelerometers and clocks in rotating and gravitating systems to be analogous.

The deeper connection that Rotonians suspect exists between Eq. (3) on one hand, and Eqs. (4) and (5) on the other, is yet to be spelled out. As a preview, note that the explicit appearance of time $t$ in Eq. 3 indicates a constantly increasing velocity through space. The ever-increasing speed of the rocket indicates a state that is clearly neither static nor stationary, because the magnitude keeps changing (monotonically). This means that a clock on the accelerating rocket would tick at an ever decreasing frequency.

The clock-rate expressions (4) and (5), by contrast, indicate two analogous, though crucially different kinds of stationary motion.[13-15] Eq. (5), concerning uniform rotation, also represents the effect of motion through space, because the direction keeps changing (periodically). The motion may nevertheless be called stationary because the speed, distance from the axis, and clock rate all remain constant. Whereas Eq. (4)—if the velocity in its argument is physically real—must represent not motion through space, but rather stationary motion OF space. This important distinction, and further consequences of the idea of stationary gravitational motion, will be recurring themes in what follows.

4.2. Energy Non-Conservation. The above facts, equations, figures, and ideas are among the clues that Rotonians have gathered about this newly discovered phenomenon called gravity. Similar to the experience of the Earthian physicist Albert Einstein, Rotonians feel especially encouraged by the extent to which the analogy between rotational motion and gravitational motion holds true.[16] Clearly this is something to build on and explore; to discover the limits of the analogy’s applicability; to discover those areas where the analogy breaks down; to bring in new ideas as needed; and ultimately to test this whole line of thought by experiment.

As suggested above, Rotonians see Eq. 3 as a key to building the rotation analogy further than Earthians have done, and generally, as a pivotal element in assembling gravity’s many facets into a coherent picture. The limiting function of light speed for motion due to constant linear acceleration (as expressed by Eq. 3) inspires the Rotonian idea that it has a similar function with respect to gravitational motion. A little more background is needed before presenting the details of how Rotonians adapt the equation to deduce its gravitational counterpart. Suffice it for now to point out that Rotonian logic is anathema to Einsteinian logic. Einstein would never have dreamed of the connection as long as he remained faithfully dedicated to the presumptions of self-rest and staticness of gravitating bodies.

Seeing that the effects on accelerometers and clocks were the same in both rotating and gravitating systems, and assuming material bodies to be static things, Einstein rigorously adhered to his Principle of Relativity, on the basis of which he justified thinking of the rotating system as also being at rest.[12] Whereas Rotonians see this approach as totally absurd. Clearly it makes more sense to accept the absoluteness of rotational motion, according to which the opposite inference follows: Motion-sensing devices tell the truth about both systems. The effects are the same, so the causes are most likely the same; both systems undergo stationary motion. Rotonians feel confident that their interpretation is more logical. Whether this is true or not remains to be discovered by experiment. To give a broader picture of the Rotonian reasoning, we need first to digress—to widen our context and to address a few objections.

From the tradition-steeped Earthian perspective (whereby all motion may be—at least “locally”—relativized to a state of rest) one of the foremost objections to the Rotonian perspective concerns the energy conservation law. Rotonians are well aware that their prediction for Galileo’s experiment, if confirmed, would violate this law. The most immediate defense is simply that Conservation of Energy has not yet been tested inside matter. It remains to be seen whether or not the law holds up in the case of gravity-induced radial motion through the centers of material bodies. Is this not all the more reason to conduct Galileo’s experiment? The Rotonians’ working hypothesis, in a nutshell, is that matter is a source of perpetual propulsion and the perpetually active source of space. As far as they can tell, this is what gravity is. The hypothesis goes quite naturally with the idea that energy is always increasing.

In most cases involving mechanics, thermodynamics, electromagnetic and nuclear forces, and exterior gravitational fields, energy will appear to be conserved, as proven by experience. Rotonians nevertheless interpret the evidence as indicating that energy non-conservation would be revealed by conducting an experiment that tests for gravity-induced motion inside matter. Ideally, Earthians would have already performed this experiment and analyzed its results. But they have not. Rotonians need to acquire the data anew. While awaiting fabrication of the apparatus, Rotonians continue fleshing out their hypothesis on the basis of existing evidence and simple physical and geometrical reasoning—all of which they see as supporting their prediction.

It should be mentioned that the status of the energy conservation law in GR—even among standard theorists—is sometimes discussed as being controversial, questionable, and certainly more complicated than its straightforward treatment in Newtonian gravity. This is especially true with regard to standard cosmology. For example, the recently inferred accelerated expansion of the space of the cosmos (as discontinuous from the matter of the cosmos) is often regarded as indicating that, globally, energy is increasing. Space supposedly creates ever more of itself—independent of matter—increasing the speed with which the galaxies supposedly recede, thereby increasing global energy.

The SGM, by contrast, attributes the increase of space to the stationary motion of localized bodies of matter (as continuous with space)—which is gravity. This model thus provides a more intuitive, physically sensible, and more directly testable picture of accelerated cosmic expansion. We’ll return to this idea later.

4.3. Spatial and Physical Dimensions: Phase 1. Perceiving how radical their energy non-conserving hypothesis must be in the eyes of most Earthians, the Rotonians understand that it could not possibly be true if there were only three dimensions of space. The basis of the Rotonian scheme is that accelerometers always tell the truth. But this makes no sense for acceleration along their planet-planted towers, for example, if one tries to naïvely envision the acceleration as an expansion in (3+1)-dimensional spacetime.[17] As per the inverse-square law, the acceleration at $r=R$ is four times what it is at $r=2R.$ In (3+1)-dimensional spacetime the indicated accelerations would cause the system to disintegrate.

Enter a fourth spatial dimension and the idea that accelerometers tell the truth becomes a logical possibility. [A discussion similar to the following is found in Light & Clocks.] Due to its importance, we will walk through the basics and go into some detail. The rest of this section will serve as an introduction to spatial and physical dimensionality. Section 5 will serve as an interlude that introduces a few issues whose connection to our dimensionality exposition may not be immediately obvious: The nature of Time, Unification, empirical evidence in support of GR, and invoking the Rotonian viewpoint as a marketing strategy. Having thus briefly widened the cast of our net we will then return, in Section 6, to dimensionality issues.

Our purpose here is not only to distinguish the novel SGM treatment of extra dimensions from the curiously wide range of more or less standard treatments, but to make it as clear as possible that, among our options, the SGM approach is the most compellingly physical and sensible one. We will start with some common observations, analogies, and geometrical images. The voluminous literature on the subject encompasses mathematical, physical, and even “spiritual” ideas. It often appeals to fictional anecdotes and scenarios intended as analogs of our actual or possible experience.

As Rotonians are well aware, (3+1)-dimensional thinking pervades our psyches; envisioning a fourth spatial dimension therefore does require a vital imagination. But Earthian literature exhibits a lot of confusion with regard to which of the many hyper (and even “reduced”)-dimensional ideas may have physical import and which of them may not. After briefly describing some of these popular ideas, our first task will have the negative character of ruling out most of them. We argue that such ideas may have mathematical validity or entertainment value, but are not candidates for serious physics. Ultimately, we will salvage the physically useful elements and re-synthesize them into a more coherent set of ideas and images that connect hyper-dimensionality to gravity in a uniquely Rotonian way.

Unlike typical discussions on the subject, ours endeavors to be insightful for its emphasis on the relationship between purely geometrical, i.e., spatial dimensions, and the elementary dimensions of physics. The latter, Mass ($M$), Time ($T$), and Space ($L$), are often symbolized as here. Newton’s constant $G,$ for example, may be represented by the dimensions $G \rightarrow L^3/MT^2\,.$ The SI units are cubic meters per kilogram per seconds squared. In unitless words, this can be taken to mean: acceleration of volume per mass. It will be argued that all spatial and physical dimensions (and powers thereof that play a role in describing the physical world) are utterly dependent on the others. They comprise an ultimately seamless continuum wherein no one dimension—whether geometrical or physical—can exist without all the others (unification).

An “extra” spatial dimension means having a new direction in which to move.[18, 19] A common device used in the extra-dimensional literature to help visualize extra dimensions and the relationship between spatial dimensions in general, involves imagining the experience of a community of creatures who inhabit a lower-dimensional world, such as a spherical surface. Let’s call these (2+1)-dimensional surface-dwellers, TwoWorlders. The idea is that the experience of TwoWorlders in trying to conceive of a world of three spatial dimensions may be analogous to our experience as ThreeWorlders, in trying to conceive of a world of four spatial dimensions. Our exploration will at times even reach all the way back to OneWorld. As we delve back and forth between these imaginary realms, a caveat is in order: It is imperative that we remain cognizant of the difference between dimensions as separable abstractions and the ultimate inseparability of the physical world. We must endeavor to discern those aspects of hyper and infra-dimensionality that make only mathematical sense from those that have some potential to make physical sense.

The first category of extra-dimensional thinking to be considered—as we will come to call it—is the Geometric Purist school. Though largely unphysical, it is rich with implications, some of which do lend themselves to physical insight.

4.4. Dimensionality a la Sagan. The late Earthian astronomer Carl Sagan provided a thought-provoking illustration. In his well known book, Cosmos, Sagan contemplated the same analogy as specified above. After describing certain mathematical properties of (his version of) TwoWorld, and TwoWorlders’ attempts to conceive of a world of three spatial dimensions, Sagan applies analogous reasoning to what he purports would be our experience as ThreeWorlders trying to conceive of a world of four spatial dimensions:

“If a fourth-dimensional creature existed it could, in our three-dimensional universe, appear and dematerialze at will, change shape remarkably, pluck us out of locked rooms and make us appear from nowhere. It could also turn us inside out.”

[Cosmos, Carl Sagan (Random House, 1980) pp. 262-264.]

It is worthwhile to question the basis and validity of this assertion in some detail. In the same vein as many other accounts (tracing back to the original Flatland, by E. A. Abbott, 1884) Sagan sees fit to describe how a ThreeWorlder is supposed to be able to “pluck” a TwoWorlder from a locked room on her surface, and place her back on the other side of a TwoWorld wall. This is an impossible feat for an unplucked TwoWorlder because—among other reasons—we are tentatively accepting the meaningfulness of the distinctions between TwoWorldian walls and rooms, and flat creatures living thereon. A wall wouldn't be a wall if it did not prevent passage through it.

For the purpose of the story we are also suspending our disbelief about how TwoWorlders move across their surface. The surface is understood to have no thickness. Without thickness there can be no matter and therefore no forces to provide any way to cohere or to propel oneself. Never losing sight of the story’s aspects of pure fantasy, we go along with it for its redeeming aspects, which will become evident in due course. The key aspect for the moment is that TwoWorlders’ movements are ordinarily confined to the surface; TwoWorlders cannot of themselves move perpendicular to it; they cannot pluck themselves out of the surface. Note that this power of a meddling ThreeWorlder to disconnect a TwoWorlder from the surface and put her back also allows the possibility of flipping the hapless creature so that she suddenly returns not only at a different location, but as a mirror image of her original self.

Also discussed by Sagan is the idea of interpenetration of a ThreeWorld entity as by passing through TwoWorld’s surface. If the ThreeWorld entity is a solid sphere, then, as the story goes, its initial appearance in TwoWorld would be that of a tangent point; the point then grows to a circle with a maximum size before shrinking back to a point and disappearing again altogether.

The quoted passage about plucking three-dimensional entities out of locked volumetric rooms, making them “appear from nowhere,” etc. is supposed to be directly analogous to the experience of TwoWorlders who are at the mercy of higher-dimensional ThreeWorlders. It is supposed to be equally easy, according to Sagan, for a ThreeWorlder to remove and relocate a TwoWorlder from and back to some new location on her surface as it is for a FourWorlder to remove and relocate a ThreeWorlder, for example, from a locked bank vault back to the street outside. Please bear in mind that these analogies were presented by Sagan as facts of the “third physical dimension” and a possible “fourth physical dimension.” [My emphasis.] Sagan did not suggest any need to distinguish mathematical abstraction from physical possibility. Simple reflection on the matter reveals that the described scenarios are indeed only fantasies that depend on the possibility of extracting one dimension from the others and ignoring the material characteristics of actual physical objects.

4.5. Mathematical Logic vs Physical Logic. Misconceptions arising from such scenarios trace back to the fact that lower-dimensional entities are not physically real—none of them. In physical reality there is no such thing as a two-dimensional “surface.” Countries on a globe, for example, appear as such only by virtue of extending into the third dimension at least as far as a layer of ink. The map is an abstraction which is never to be mistaken for the territory. You cannot do to the territory what may be easily done to a map, and easier still to the mental idea of doing something to a map (like making a spherical body go through the “plane” of the paper without tearing it). Surfaces are abstractions which themselves and whose sub-units cannot be “plucked” off of, or in any other physical way be extracted from the wholes in which they are imagined to reside. This means the same applies for lines and points: only abstractions. For reasons to be presented below, it is arguably also true for seemingly three-dimensional [and even (3+1)-dimensional] entities. In order to qualify as having physical pedigree, any geometrical (spatial) entity must also exhibit properties of the physical dimensions, matter-energy and time.

Based on the above reasoning and absence of any evidence to the contrary, we may logically conclude that extraction of one dimension from the others is physically impossible. So too, for intersection or interpenetration. The TwoWorld+ThreeWorld example of a solid sphere appearing and disappearing by “passing through” the surface may be mathematically reasonable and fun to visualize but it makes no physical sense. The surface through which the sphere is passing doesn’t really exist. It stands to reason (by analogy) that the higher-dimensional ThreeWorld+FourWorld counterpart is also nonsense. (4+1)-dimensional creatures will never magically pop into our seemingly (3+1)-dimensional world because it would never be possible for them to pop out of our world in the first place. We can imagine anything we want; but a good physicist—lest she wind up barking up one of the infinitely many wrong trees—will exercise judicious restraint when tempted by the fantastic world of mathematics.

Finally, a TwoWorlder being “flipped” over by a ThreeWorlder is analogous to a ThreeWorlder being turned inside out by a FourWorlder. Both scenarios are physically non-sensical because they require the lower-dimensional entity to be momentarily transferred (plucked) from the lower, into the higher-dimensional space to be transformed, and back again. As discussed above, though mathematically conceivable, this is physically impossible. The thing to be “dimensionally plucked and transformed” is just an abstraction.

4.6. Wide Range of Dimensional Ideas. The literature on extra-dimensionality is full of fanciful ideas like these that may have mathematical meaning, but make no physical sense. The TwoWorld/ThreeWorld scenarios, as noted above, may be characterized as stemming from the “Geometric Purist” school, for its way of conceiving the fourth spatial dimension. This approach emphasizes that which is mathematically true about relationships between purely geometrical objects and dimensions, whether or not these truths have any bearing on the physical world.

A brief rundown of other “schools” of extra-dimensional thought should also be given here. (Further detail will be given in §6.) Among Earthian physicists, the most popular school envisions extra dimensions as having tiny “compactified” sizes. Tracing back to the original 1920s work of Kaluza and Klein, these schemes smack of artificiality and arbitrariness. (See Figure 7.) Proponents of this school see fit to “tack on” a plethora of tiny circular dimensions to every point in otherwise (3+1)-dimensional spacetime.

A less popular, but persistent school of (4+1)-dimensional gravity was largely founded a few decades ago by the recently deceased Paul Wesson. Though sometimes regarding the fifth dimension as “large” and as pertaining specifically to matter, this approach suffers (as the Rotonians see it) because over virtually all accessible scales of the Universe, it regards GR as being essentially accurate—even inside matter—where it has not yet been tested, where Rotonians have a strong hunch that it fails. Nor does this approach address the mechanism by which matter curves spacetime. What does matter DO to cause non-zero accelerometer readings? If deviations from GR are assumed to be so tiny or non-existent, then why bother “tacking on” any extra dimensions? Rotonians suspect that incrementally adjusting existing theories (by adding virtually unobservable extra dimensions, for example) is not a sufficiently radical strategy. The ailments of fundamental physics arguably call for something more like a complete overhaul. It needs rebuilding, not from the ground up, but from the center of the ground up.

Next, two other schools of thought—whose ideas apply to opposite extremes of size—purport that it makes sense to regard the world as having not one more, but one (or two) fewer dimension(s): The so-called “Holographic Principle” involves reducing large-scale spacetime dimensions by one. The “Vanishing Dimensions” hypothesis involves reducing small-scale dimensions by two. The first of these approaches, described by Scientific American as

“...favoring antirealism is the holgraphic principle that [Leonard] Susskind and Nobel laureate Gerard ’t Hooft of Utrecht University formulated in the mid-1990s. It holds that what happens in any volume of spacetime can be explained by what happens on its boundary. Although we usually think of objects as zipping around three-dimensional space, we can equally well think of them as flattened blobs sliding across a two-dimensional surface.” — [‘Bad Boy of Physics,’ Scientific American, Jul. 2011, p.82.]

Although Susskind and others have often suggested that the Holographic Principle applies to the whole Universe, in the end one of its proponents (Juan Maldecena) admits: “It is not clear how to define a holographic theory for our universe; there is no convenient place to put the hologram.” [‘The Illusion of Gravity,’ Scientific American (Nov. 2005) p. 63.]

At the opposite extreme in size, we find a school of theorists who favor the idea that, as we consider smaller and smaller sizes (and higher and higher energies) the number of dimensions decreases down to a line (+ time). With dismay, Rotonians note that such desperate ideas are taken seriously in Earthian academies.  The “early” Universe is just a line??? Entertaining as such ideas may be, Rotonians find little else to redeem them.

Finally, we have the standard classical idea, adhered to by most dyed-in-the-wool General Relativists, that spacetime consists, quite sufficiently, of only (3+1) spacetime dimensions.

Common to all the above schools of extra-dimensional thinking (that purport to have physical relevance) is the standard idea that spatial dimensions are independent of the imaginary agents that are supposed to “mediate” physical forces. Extra dimensions are conceived, basically, as enlarging the conduit across which forces are imagined to spread and travel. They are not supposed to have any more intimate a relationship than that. In other words, extra dimensions are supposed to exhibit a greater quantity of static volume for the fragmentarily conceived forces of matter to move through.

To illustrate, if an extra dimension were “large,” it would supposedly “dilute” any forces propagating through it, depending on the extra dimension’s exact size.  For example, if the size of a fourth spatial dimension were 1 cm, then for distances smaller than 1 cm, the attractive force of gravity would supposedly fall off, not according to an inverse-square law, but according to an inverse-cube law. If extra dimensions were “small,” then we can have lots of them, because their diluting effect would be more widely distributed and more well hidden among multitudes of grotesque Planck-scale Calabi-Yau crumple manifolds, as in Figure 7—where math-geekery runs rampant and observational evidence plays no role whatsoever. Whether large or small, unfurled or crumpled, “standard” extra dimensions leave unchanged the primitive concept of gravity as a mysterious attractive force, operating through space (“telling matter how to move,” etc.).

Rotonians regard all these schemes as woefully inadequate and unphysical because they do nothing to address, much less conclusively establish what Rotonians think of as the first—or even zeroth—thing that needs to be known about gravity: its direction, as indicated by accelerometer readings. Should accelerometers be believed or not? Earthian theorists either equivocate on this question or (more commonly) presume the answer is contrary to what accelerometers actually say—as discussed above and in Sidenote [11].

The standard conceptions of spacetime dimensionality are in stark contrast with the embryonic Rotonian hypothesis (SGM) whereby space serves not as a kind of vacuous, discontinuous arena across which forces are “mediated.” Rather, space is a product of the activity of matter. That gravity manifests itself according to an inverse-square law is a natural consequence of space emanating from, and being acceleratively produced by every continuous material source.

Why should a “holographic” surface be conceived as representing the whole dynamically volumetric Universe? As a bizarre mathematical plaything perhaps, not physics. Why should a dimension have a small size? The main reason is to make it so small that we can’t see its effects. Even Einstein recognized this as an insufficiently good reason.[20] A sub-group of theorists who work on these ideas think that by invoking a handful of extra dimensions whose size may be just on the threshold of detectability, they can explain the weakness of gravity. Gravity would be much stronger, they argue, were it not diluted by being distributed over a Calabi-Yau-crumpled bunch of not-quite-unreachably small extra dimensions.

Their endeavors are implicitly justified by adjusting the size/number of dimensions to be just barely detectable in particle collision debris or other delicate experiments. So far observations have come up empty. For whatever reason, strings, branes, gravitons, and crumpled extra dimensions yet remain the concerns of many modern scholars who purport to be doing research on gravity.

Would a tiny accelerometer following the contour of a crumple give a zero or non-zero reading? Either way, what are such bizarre things supposed to DO to cause gravitational attraction between massive bodies? The absence of sensible answers to simple questions like this give Rotonians the impression that the whole enterprise is an absurd—though perhaps vaguely entertaining—exercise in unphysically abstract futility. Rotonians not only refuse to be distracted by the bizarre hyper-dimensional ideas of mainstream Earthian academicians, they have adopted, as a kind of antidote to them, the following guiding principle:

Any localized portion or sub-unit of a physical continuum such as our Universe has the same dimensionality as the whole Universe.

This succinctly reiterates conclusions already drawn: It is not possible to physically extract (or compactify) one dimension out of the others. Hiding extra dimensions for no good physical reason makes no sense. Equally non-sensical is the notion that the actual dimensionality of the Universe is smaller than what we have empirically established to be a minimum (3+1). By holography or “dimensional reduction” some complex phenomena may perhaps be rendered more mathematically tractable, but it is inappropriate for modelling the global, all-inclusive world.

The existence of an extra dimension ought not to be presumed, of course, without compelling (or at least suggestive) evidence. And then we had better devise a way to reveal or empirically explain it. Otherwise it is not physics. As noted above, many physicists entertain the notion that evidence of (compactified or warped) extra dimensions may be buried in the Large Hadron Collider’s particle collision debris—as some tiny deviation from standard predictions. Both the predictions and the search are endeavors of extreme complexity, if not monetary cost. Yet these physicists continue to neglect to test their predictions in the simple, direct, and relatively inexpensive physical domain inside ordinary bodies of low-energy matter.

By the Rotonians’ guiding principle, the dimensionality of a “realistic” TwoWorlder is exactly as high as theirs (and ours). Note that this is exactly the point made by Ouspensky.[21] We are not as gods to lower-dimensional creatures; and we are not at the mercy of any physically real FourWorlder, because if FourWorlders exist, we are them. And if we are them, we must find out, as Ouspensky also states, “in a purely experimental way.”

This raises the question, is (3+1)-dimensionality sufficient to insure physicality? Does it make sense to conceive of one temporal and three spatial dimensions as having some kind of independent existence? If the world is actually (4+1)-dimensional, then the answer is obviously no. If curvature of (3+1)-dimensional spacetime requires one more dimension to curve into (as implied by our TwoWorld analogy) the answer is also no. Something essential is missing. Even (3+1)-dimensionality is just abstract geometry, not physical reality. Allowing time is a step in the right direction. But to be physical there must also be matter. By making (3+1) spacetime dimensions curve, the existence of gravitating matter thereby implies that one more spatial dimension is also needed; it implies that matter, space, and time are interdependent elements.

Rotonians see the pronounced directionality of not just time, but all three elements as evidence that adding a dimension is still insufficient, if it is supposed to be static. The word making (in the above sentence) is a verb. An “extra” dimension means having a new direction in which to move—another verb. Combining ideas, Rotonians conceive that matter makes spacetime curve because it is perpetually moving, it is actively generating space, by moving into (or outfrom) a fourth spatial dimension. This is the essence of gravity. If we are to go beyond abstract mathematics, the two senses of the word dimension—the purely geometric/spatial and the physical—must be merged; they need each other. The physical elements of time and matter require at least three (and arguably four) spatial dimensions and vice versa. Rotonians deduce that—in order to exist at all—each of the “first” three dimensions of volumetric space require time, matter, and a fourth spatial dimension. The Universe, and every seemingly separable thing in it, is an interdependent, all-or-nothing package deal. And nothing is not really an option.

Section 5